OUTPUT LEVEL
FILTER CONTROLS
4000-Pole Allpass Filter
A JavaScript-based implementation of an extremely high-order allpass filter capable of generating 4000 poles. The filter is constructed of 2000 cascaded second-order allpass Biquads, with real-time stochastic parameter modulation (jitter) affecting both frequency and resonance. This gives a massive 24,000 dB per octave slope, designed for extreme phase manipulation of audio signals.
1. Theoretical Foundation of Allpass Filtering
An allpass filters are a unique class of linear time-invariant (LTI) systems characterized by a unity magnitude response across all frequencies while introducing frequency-dependent phase shifts.
Allpass filter do not subtract or add freqeuncies like a low or high pass filter. They only affect the PHASE of a signal. They are often used to compensate the phase changes caued by other filters eg: in speaker crossovers.The fundamental property of an allpass filter is expressed mathematically as:
where H(ω) represents the frequency response. The phase response φ(ω) = arg[H(ω)] varies continuously with frequency, creating the characteristic temporal displacement effects associated with allpass filtering.
1.1 Second-Order Digital Allpass Transfer Function
The implementation utilizes second-order allpass sections with the canonical transfer function:
This can be rewritten in terms of filter parameters as:
where r represents the pole radius (related to Q factor) and θ represents the pole angle (related to cutoff frequency). The relationship between these parameters and the traditional filter specifications follows:
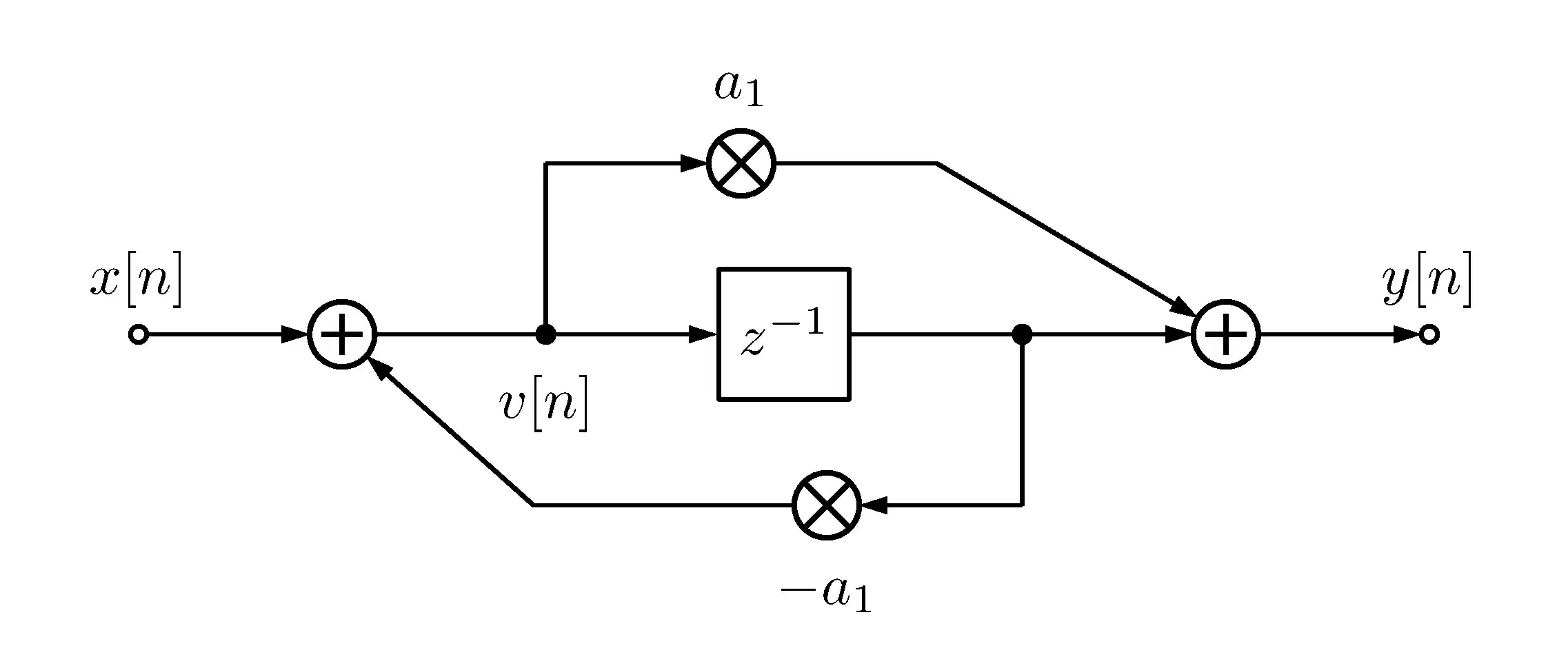
2. System Architecture and Signal Flow
The complete signal processing chain implements a cascaded topology where each processing stage contributes specific functionality to the overall system response. The architecture follows a modular design pattern enabling independent control of each processing element.
2.1 Filter Bank Implementation Strategy
The JavaScript implementation creates a cascaded filter bank where each second-order allpass section contributes two poles to the overall system response. The total system order N_total = N_sections × 2, enabling configurations up to 4000 poles through 2000 cascaded biquad sections.
3. Stochastic Parameter Jitter Analysis
The jitter system implements real-time stochastic modulation of critical filter parameters, creating time-varying system characteristics that fundamentally alter the phase response behavior. This represents a departure from traditional static filtering toward dynamic, probabilistic signal processing.
3.1 Mathematical Model of Jitter Implementation
The jitter system modulates two primary parameters: the cutoff frequency f_c(t) and the quality factor Q(t), according to the following stochastic processes:
where f_c₀ and Q₀ represent the base parameter values, A_f and A_Q are the jitter amplitude coefficients, and ξ_f(t) and ξ_Q(t) are independent white noise processes with uniform distribution over [-1, 1].
3.2 Temporal Smoothing Implementation
The smoothing parameter τ controls the transition behavior between parameter updates, implementing either discrete jumps (τ = 0) or exponential interpolation (τ > 0). The Tone.js framework provides native support for parameter ramping through the exponentialRampToValueAtTime method:
4. Phase Response Analysis
The phase response of the cascaded allpass system exhibits complex behavior that fundamentally differs from traditional filtering approaches. Each individual second-order section contributes a phase shift that varies continuously from 0° to -360° as frequency increases from DC to Nyquist.
4.1 Individual Section Phase Response
For a single second-order allpass section, the phase response is given by:
where ω₀ represents the natural frequency and ζ the damping ratio. The total phase shift for N cascaded sections becomes:
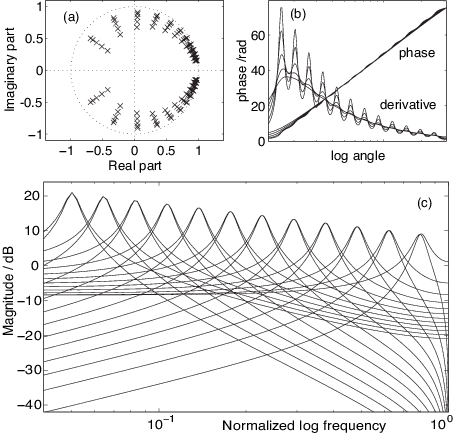
4.2 Group Delay Implications
The group delay τ_g(ω) = -dφ/dω represents the frequency-dependent time delay introduced by the allpass filtering process. For high-order systems, this creates significant temporal dispersion:
At maximum configuration (4000 poles), the group delay can reach several milliseconds, creating audible temporal smearing effects that fundamentally alter the perception of transient events in the audio signal.
5. Computational Implementation Details
The JavaScript implementation leverages the Tone.js framework’s native biquad filter implementations, which utilize optimized Web Audio API AudioNode connections for real-time processing.
| Parameter | Range | Implementation | Update Method |
|---|---|---|---|
| Cutoff Frequency (f_c) | 20 Hz – 20 kHz | Tone.Filter.frequency | exponentialRampToValueAtTime |
| Quality Factor (Q) | 0.1 – 20 | Tone.Filter.Q | linearRampToValueAtTime |
| Filter Order (poles) | 2 – 4000 (even) | Array of Tone.Filter | Reconstruction |
| Jitter Rate | 0.001 – 100 Hz | setInterval timing | Dynamic interval |
| Jitter Smoothing | 0 – 1000 ms | Ramp duration | Parameter to ramp methods |
5.1 Memory and Computational Complexity
The computational complexity scales linearly with the number of filter sections. Each second-order section requires storage of two delay elements and multiple coefficient calculations per sample. The total computational load per sample becomes:
where N_mult represents multiplication operations, N_add represents addition operations, and N_mem represents memory accesses per biquad section.
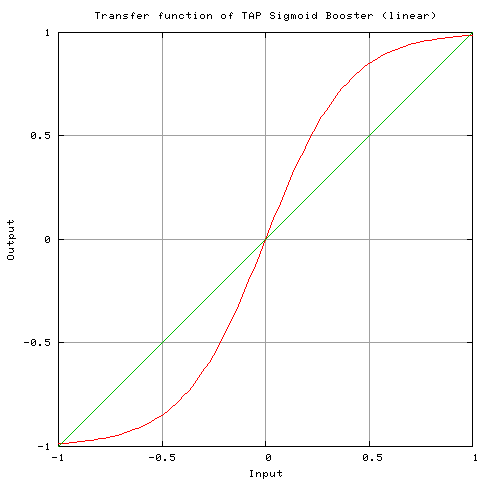
6. Nonlinear Processing Chain
The soft clipping stage implements a hyperbolic tangent waveshaper, providing controlled harmonic distortion that complements the phase manipulation effects of the allpass filtering:
7. Real-Time Performance Considerations
The extreme filter orders achievable in this implementation present significant challenges for real-time audio processing. The Web Audio API’s native optimization becomes critical for maintaining acceptable latency and preventing audio dropouts.
7.1 Buffer Management and Latency
Each filter section introduces minimal individual latency, but the cumulative effect of 2000 cascaded sections creates measurable group delay. The system must balance filter order against real-time performance requirements:
where L_biquad represents the latency per biquad section and L_jitter_update accounts for parameter update overhead.
8. Psychoacoustic Effects and Perceptual Implications
The extreme phase manipulation achieved through high-order allpass filtering creates psychoacoustic effects that extend beyond traditional audio processing paradigms. The human auditory system’s sensitivity to phase relationships becomes evident through several perceptual phenomena:
Spatial Displacement: The frequency-dependent group delay creates apparent movement of spectral components in the stereo field, even in monophonic signals.
Temporal Smearing: Transient events become temporally dispersed, creating unique rhythmic and textural effects that can enhance or degrade musical material depending on context.
Harmonic Decorrelation: The differential phase shifts applied to harmonic components create timbral changes that preserve spectral energy while fundamentally altering harmonic relationships.
9. Comparative Analysis with Traditional Filtering
Unlike conventional lowpass, highpass, or bandpass filters that modify the magnitude spectrum, this allpass implementation operates exclusively in the phase domain. This fundamental difference enables unique processing capabilities:
Traditional filters create frequency-selective attenuation or amplification, while allpass filters create frequency-selective temporal displacement. The mathematical relationship between these approaches can be expressed through the complex frequency response decomposition:
where traditional filters modulate |H(ω)| and allpass filters modulate φ(ω) exclusively.
10. Conclusions and Future Directions
This implementation represents an extreme exploration of allpass filtering capabilities, pushing the boundaries of what is computationally feasible and perceptually meaningful in digital audio processing. The combination of extreme filter orders with stochastic parameter modulation creates processing effects that would be impossible to achieve through analog means.
The system demonstrates that phase-only processing can create dramatic audible effects while preserving the fundamental energy content of audio signals. This approach opens new possibilities for audio effects processing, spatial audio manipulation, and creative sound design applications.
Future research directions might include investigation of using high order allpass filters to create pitch shifters / chorus / time modulation effects.
11. Technical Specifications Summary
| Specification | Value | Notes |
|---|---|---|
| Maximum Filter Order | 4000 poles | 2000 cascaded biquad sections |
| Frequency Range | 20 Hz – 20 kHz | Full audio bandwidth |
| Q Factor Range | 0.1 – 20 | Subsonic to extreme resonance |
| Jitter Update Rate | 0.001 – 100 Hz | Glacial to audio-rate modulation |
| Processing Precision | 32-bit float | Web Audio API standard |
| Maximum Group Delay | ~10-50 ms | Frequency and order dependent |
[1] This analysis is based on the JavaScript implementation utilizing Tone.js framework v14.8.49
[2] Mathematical models assume ideal biquad implementations without quantization effects
[3] Performance characteristics may vary significantly based on browser and hardware capabilities
[4] Extreme filter orders may cause audio dropouts on resource-constrained systems
[5] The stochastic jitter implementation uses JavaScript’s Math.random() for simplicity rather than cryptographically secure random number generation